NM156
Member
I recently heard conversation by a young model enthusiast who stated "Why do I have to learn math in school, I'll never use it".
Personally I have always found that real world examples tend to validate the learning experience.
If you are a builder, maker etc., you most certainly will use math to various degrees. In fact I would guess that most of you already know that. But here is something that could be used as a STEM demonstration that is a simple and practical, but effective, use of trigonometry.
(To make things easier, we'll just work in degrees and ignore the use of radians).
Example 1 (top)
Example 2 (bottom)
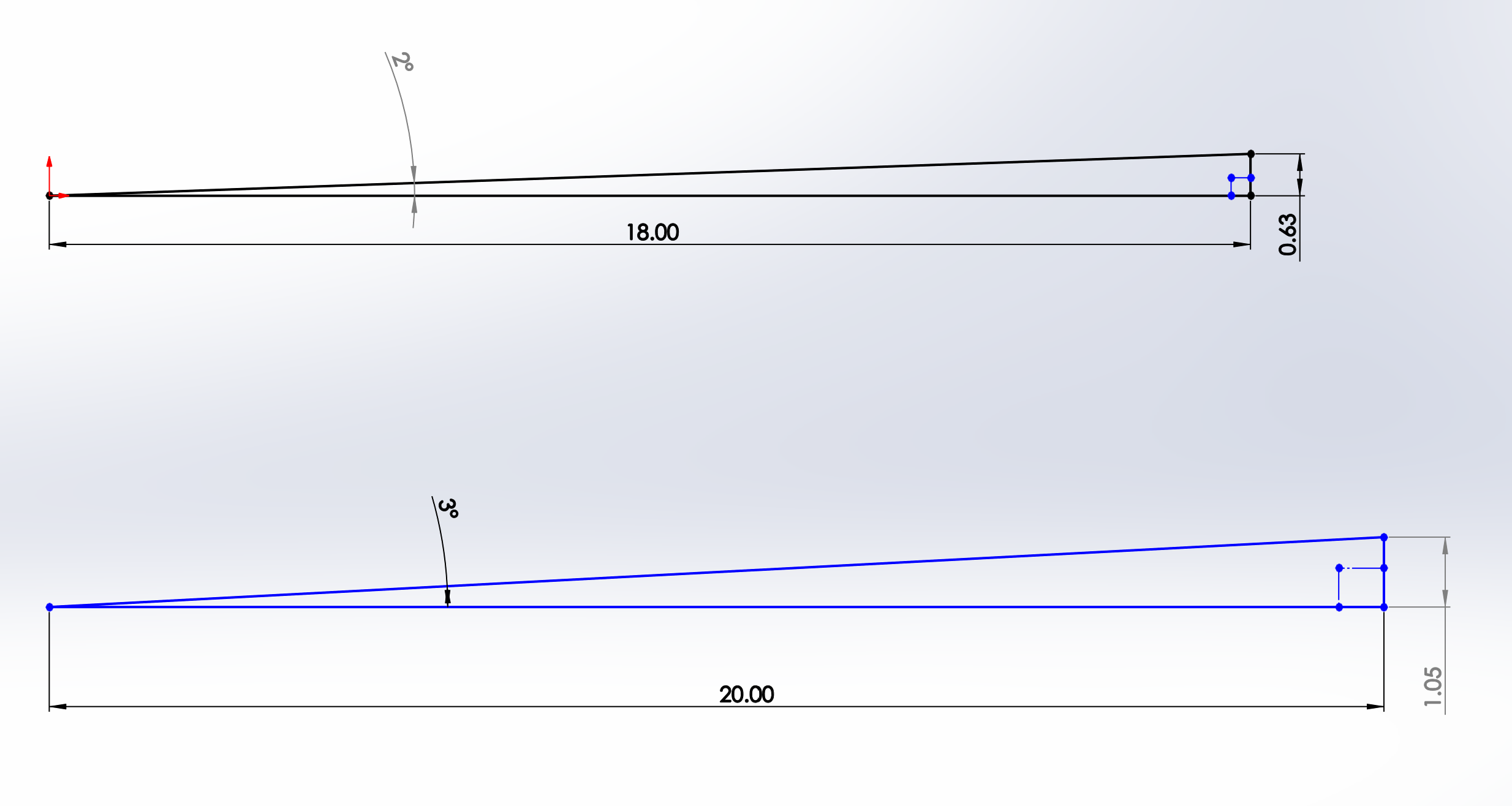
EXAMPLE 1:
How much dihedral does your 36" wing have?
Place the wing on a table with one side resting on the table. A triangle is formed between the table, the lower wing surface and the wingtip height from the table.
The adjacent side is half of the wingspan. 18 inches.
The opposite side is the height of the bottom of the tip to the table. 0.63 inches
To solve we will use the arc tangent (inverse) function.
atan(opposite / adjacent)
atan(0.63 / 18.0)
atan( 0.035 ) = 2.00
The answer is 2.00 degrees of dihedral.
EXAMPLE 2:
You want to have 3 degrees of total dihedral in your wing, how high should the tip be when the wing halves are joined?
Assume a 40 inch wing span. Again we will use the tangent function, since we are still using the opposite and adjacent sides, but this time we have an angle supplied.
tan(dihedral) * (wingspan/2)
tan(3) * 20 = 1.047
The answer is to raise the wingtip 1.047 when joining the halves.
PS
The arctan function is available on the Windows calculator in "Scientific" mode under "Trigonometry" when 2nd is depressed. (tan-1)
Ensure that the mode is in DEG.
PPS
The irony does not escape me that the example drawings were done in CAD and solved the equations!!!
Personally I have always found that real world examples tend to validate the learning experience.
If you are a builder, maker etc., you most certainly will use math to various degrees. In fact I would guess that most of you already know that. But here is something that could be used as a STEM demonstration that is a simple and practical, but effective, use of trigonometry.
(To make things easier, we'll just work in degrees and ignore the use of radians).
Example 1 (top)
Example 2 (bottom)

EXAMPLE 1:
How much dihedral does your 36" wing have?
Place the wing on a table with one side resting on the table. A triangle is formed between the table, the lower wing surface and the wingtip height from the table.
The adjacent side is half of the wingspan. 18 inches.
The opposite side is the height of the bottom of the tip to the table. 0.63 inches
To solve we will use the arc tangent (inverse) function.
atan(opposite / adjacent)
atan(0.63 / 18.0)
atan( 0.035 ) = 2.00
The answer is 2.00 degrees of dihedral.
EXAMPLE 2:
You want to have 3 degrees of total dihedral in your wing, how high should the tip be when the wing halves are joined?
Assume a 40 inch wing span. Again we will use the tangent function, since we are still using the opposite and adjacent sides, but this time we have an angle supplied.
tan(dihedral) * (wingspan/2)
tan(3) * 20 = 1.047
The answer is to raise the wingtip 1.047 when joining the halves.
PS
The arctan function is available on the Windows calculator in "Scientific" mode under "Trigonometry" when 2nd is depressed. (tan-1)
Ensure that the mode is in DEG.
PPS
The irony does not escape me that the example drawings were done in CAD and solved the equations!!!

